At its most basic level, one button starts a motor and another button stops it. The velocity of the movement is fixed by the motor's characteristics, e.g., an induction motor with a rated RPM and line frequency. Functionally, there is no position or velocity defined. Applications that fit these criteria might include motors powering conveyer belts, pumps, fans, and everyday devices found in homes such as furnaces, washing machines, dryers, or vacuum cleaners.
Many industrial applications control motion this way as well. The start-button's signal may be processed by a PLC or controlled by additional devices such as sensing switches, which may replace or augment the start or stop buttons.
More precise motion performance controls trajectory and velocity over time and specifies endpoints or distance to be traveled. In addition, two or more axes may execute simultaneously to create a composite move through space. A motor drive generates various excitation signals, phases, and frequencies that direct motors to run at variable speeds in either forward or reverse, as well as remain stationary.
Precision Motion Principles
This article covers the principles and execution mechanisms of precise motion control. A thorough review of these principles may permit readers a chance to better understand the high-level programming capabilities of current motion control technologies and apply them practically, i.e., collecting motion commands, graphically describing trajectories (defining the cutting paths from raw stock to finished part), or programming a robot, to name just a few.
This article also describes how a PC may be used to precisely control motion over several axes. In this case, the actuators may be independent single axes, three-linear-axes systems typically found on milling machines, or sophisticated five-axes systems found controlling robots with articulating or jointed arms.
The control algorithm defines the move of each axis as a function of time and then computes the trajectory in increments of time or [Delta]t. In accordance with a sensible division of computing labor, only a few, simple motion controllers close some of the above-mentioned low-level loops in the PC, while most other motion controllers handle the loop closures and low-level routine computations of one or more axes with separate axis CPUs.
It's All About Feedback
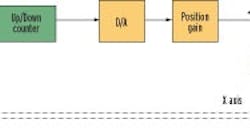
The feedback loop is a key element of precise motion control and has to be in place before any motion commands can be executed. Figure 1 shows a feedback loop including a digital rotary encoder that provides two pulse trains, normally identified as track A and track B. These encoders provide 4,096 pulses per turn and track; so by decoding every transition, 16,384 pulses are obtained per revolution. The two tracks are resolved in a bi-directional logic, and feedback pulses are applied to an up/down counter. The contents of the counter may be applied to a digital-to-analog (D/A) converter and the resulting analog voltage serves as a signal to the drive that generates the motor excitation. In most cases, the encoder is directly and physically coupled to the motor shaft.
Figure 1: The Feedback Loop is Key
If the polarity of the feedback pulses is correct, the counter initially reset, and zero analog voltage defined as no motion, then this system of feedback will hold the motor at a standstill. Any disturbance that tries to rotate the shaft will cause an offset in the counter and thus a corrective drive signal to oppose the action. A conventional tachometer coupled to the motor's shaft could be introduced at this point to enhance the feedback system and stabilize the velocity loop, again, as long as it observes the proper polarity of the signal.
Numerical Control's Legacy
Today's sophisticated motion controls had their origin in the hardware Numerical Control(NC)Systems of the mid-1960s. In addition to the feedback loop shown in Figure 1, NC systems provided coordinated command pulse trains to the feedback loop of each axis. Each up/down counter had two more inputs: Command pulse train and sign. When command pulses were added to the counter (+ pulses), the value in the counter increased and caused a drive signal to the motor in a way that generated feedback pulses (- pulses) that subtracted from the counter again. During the move, the offset value in the counter was the following error. When command pulses ceased, the counter eventually returned to a zero value and the move stopped.
Figure 2 shows the introduction of the command pulse train. An anti-coincidence circuit assures that no pulse is lost from either source. If for example, a command (+) and a feedback (-) occur together, no count pulse is passed on to the counter. If a command (+) and a feedback (+) should occur together then the counter is incrementally advanced by two.
Figure 2: Get on the Pulse Train
Early NC systems used rate multipliers to generate pulse trains for the individual axis. Basically, a common counter chain divided a high-speed pulse source by several decades; each axis gated-out the proper number of pulses according to its programmed command. The commands for each axis were given in incremental form; as such, the value was equal to the number of pulses to be generated per move block.
Since axes data are gated from the same common divider chain, a simultaneous move results. If the high-speed pulse source changes its frequency over time, then all axes will follow in lock step, allowing for acceleration and deceleration or feed-rate override without sacrificing the programmed path. Figure 3 shows an example of a counter chain with boxes representing the gates, selected with the individual incremental axis data.
Figure 3: Coordinated Pulse Metering
Command Modulation
The common divider chain represents time, and therefore, each axis may be described solely as a function of time. Coordinated moves result because the time t is common in the parametric form of each axis:
Equation 1
x=a X t, y=b X t and z=c X t;
where a, b, and c represent the incremental distance each axis is to travel during t.
If t is expressed as total time, i.e., total number of source pulses, then a, b, and c are expressed as a fraction, e.g., t=10,000, a=0.7242, b= 0.4296, and c=0.1548. In the example, x receives 7,242, y receives 4,296, and z receives 1,548 pulses for every 10,000 time pulses; and the distribution of those pulses is equally spread over time. Figure 3 shows the coordinated pulse metering.
The velocity is determined by the frequency of the source pulses:100 KHz for example, or one source pulse every 10 seconds. The above case illustrates the familiar linear interpolator, where the values of a, b, and c do not change over time. Each axis command pulse is of the same resolution as a feedback pulse from the described digital encoder above.
Figure 2 shows the closed-loop feedback with the command modulator added. As soon as command pulses are introduced, the axis will move, traveling in steady state at the same speed as the command pulses. The axis will come to rest again after the command pulses have stopped.
Now for New Instructions
To prepare for replacing the old-school pulse-modulating hardware by the computer instruction from a PC, we rewrite Equation 1 into differential Equation 2. Each iteration in the differential form creates an incremental move.
Equation 2
x=a X t, y=b X t and z=c X t;
Here, t represents one source pulse (in the example, those pulses re-occur at 10-sec. intervals). Equation 2 is then executed, e.g., 10,000 times. If we change the very small t in Equation 2 to a larger time interval such as t=1 msec, then we have:
Equation 3
x=A X [Delta]t, y=B X [Delta]t, and z= X [Delta]t;
Since we divided the number of iterations in Equation 3 by 100, we must do the same to a, b, and c; thus A=72.42, B=42.96, and C=15.48. In other words, for one iteration at 1 msec, the axes must receive the equivalent of 72, 42, and 15 pulses with the remainders being carried forward into the next iteration. So, the up/down-counter is augmented by adders/subtractors. Even larger time intervals, such as [Delta]t=10 msec may be used, again adjusting A,B, and C respectively. This change from pulses to values will result in add or subtract instructions for a general-purpose CPU implementation.
Often, instead of providing incremental position commands ([Delta]x, [Delta]y, [Delta]z), new absolute position commands (x, y, z) are computed and provided every [Delta]t. For most general motion applications, it is sufficient to provide new x, y, and z commands for every [Delta]t. For very sophisticated or multi-axes contouring controls, velocity* and even acceleration* commands may be provided in addition to position control as denoted by * and shown on the top in Figure 4.
Figure 4: Position Feedback Replaces the Tachometer
Digital Replaces Hardware
Figure 4 shows a digital axis feedback and command control. Note that the distance traveled per [Delta]t (feedback per [Delta]t) also represents a digital tachometer value, so there is no longer a need for a physical tachometer. Basically, only the encoder, bi-directional logic, a simple up/down counter, and the velocity feedback register remain in hardware--the rest becomes CPU instructions and memory addresses. The drive is left as a box, since it is not discussed here.
In operation, the contents of the up/down counter are transferred every [Delta]t to the velocity feedback register, and then the counter is reset without skipping any count pulses. Triggered by the [Delta]t real-time interrupt, the CPU executes the various multiplications and summations. In addition to computing the path trajectory for each axis, the CPU is very busy handling the low-level axis loops every [Delta]t.
Interface Between PC and Axes
All the low-level loop closures--the position loop, velocity loop, and even the torque and drive-signal generation loops--may be handled on one axis card with a separate, local CPU. Nowadays, drives such as variable-frequency AC drives often include these loops. Therefore, the interface between PC and the axes CPUs is a line of "divide and conquer."
The task of the PC is then simply to generate the trajectory of a move, namely to generate the command stream for each axis in increments of [Delta]t and to pass it to the lower-level axis execution units. The low-level execution units then make sure the commands are tightly followed and that the servo motor is keeping up with the commands. Note that the command data includes absolute position, and, optionally, velocity and acceleration. The commanded values for velocity and acceleration may be treated as independent data and may be provided, in addition to position, for more precise motion control such as feed forward and transition control. Yet in reality, they are certainly not independent of each other. Position is indeed the integral of velocity as shown in Equations 2 and 3. Figure 4 shows in detail, and Figure 5 shows schematically the dividing line between PC and axes cards.
Figure 5: Division of Computing Labor
Configuration data such as various gain settings may be sent from the PC to the axes. Alternately, a trial move may be executed, and the axis may optimize the overshoot and settling time. This is called auto-tuning, and the axis computes, and then uses the optimal values, which may then also be read by the PC.
Application Evidence
One of the most-often-used commands in general motion control is a move from one position (present position) to a new target position. The instruction allows the user to specify the target position, a maximum velocity, and an acceleration/deceleration for the beginning and end of the move. The deceleration may be viewed as a negative acceleration of same or different value. Figure 6 shows the trajectory of the position over time, as derived from the acceleration and maximum velocity.
Figure 6: Derived Position Trajectory
At the beginning of the move, the constant acceleration--integrated over time--creates a linear velocity ramp. This velocity, then integrated, creates the position trajectory. When full velocity is reached, the acceleration is set to zero and the position follows a linear ramp. At the time of deceleration, a negative value is placed into the acceleration register such that the velocity will ramp-down linearly to complete the move. It is sufficient to transmit (at every [Delta]t) just the new position to the axis CPU, since it incorporates acceleration and velocity via the integral--unless, as in the case of multi-axes contouring, a near-zero following error is desired. In that case, auxiliary velocity and/or acceleration data may be used in addition to the position data. Figure 7 shows the trajectory generation in the PC and the register values available for transmission to the axis' CPUs.
Figure 7: Informing the Axes' CPUs
In more complex moves, the acceleration register may not be a constant. In circular interpolation (the x and y axes together describe a circle), the parameterized positions are x=R X cos t and y=R X sin t, and the parameterized velocities and accelerations are also sin/cos functions of t.

Leaders relevant to this article: