Time-Scale troubleshooter

By Michel Ruel, PE, Top ControlUsing the time scale is a novel, simple way for process equipment builders to troubleshoot misbehaving control loops when necessary. By examining each component of the relative time, you quickly can tell if the loop is operating within consistent ranges. If misbehaving, the method allows you to quickly pinpoint the problem.

A control loop consists of the process, the measurement, the controller and a final control element. Optimal process control depends on all these components working properly. So, before tuning a loop, you need to verify that each component is operating properly and the design is appropriate. Most processes behave as illustrated in Figure 1.

In manual mode (open loop), a self-regulating process (top) will reach a new stable state. An integrating process (bottom) will continue to increase or decrease at a constant rate.

A self-regulating process is a process that stabilizes itself in manual mode. A flow loop is an example of a self-regulating process. After a controller output change in manual mode, the process will reach a new stable state.

Some processes will not stabilize after a controller output change, but instead will increase or decrease at a constant rate. These processes, called integrating processes, also are encountered and consist mainly of pressure or level loops.

Most processes can be modeled using these two categories. If not, the model needs to have more parameters.

Time Defined

To further discuss the time scale, it is important to define certain time parameters:

Dead time (t_d) corresponds to the elapsed time after a controller output change, before the process variable starts to move. This elapsed time can be observed in manual or automatic mode; the dead time greatly reduces control-loop performance and the speed of response.

Time constant(τ) is the time required to reach the final value if the actual speed (slope) was maintained. This applies to self-regulating processes after a bump test in manual mode. The time constant is also the time to reach 63% of the remaining amplitude. These two definitions are true on any part of the curve corresponding to the time constant, after the dead time.

For an integrating process, the time constant is replaced with the integrating time. The integrating time is the time needed for an amplitude change of the same magnitude as the controller output.

Settling time (t_set in automatic mode) is the time needed for the process value to reach the setpoint and to remain close to it. The closeness is usually defined as within a 5% band from the total change.

Damped period (t_osc)happens if the controller is tuned too aggressively in automatic mode. Cycling will appear after a setpoint change or a disturbance, but will disappear gradually. This will appear as a damped sine wave.

Sampling time (t_s) is the time it takes to recalculate the controller output; it also is called the update time. To ensure the digitized controller will behave almost as an analog controller, the update time must be short.

Prepare to Tune

Controller tuning is defined as adjusting the tuning parameters so the control loop will meet the performance criteria allowed by the process. Tuning a loop implies the transient response after a setpoint change or after a load change will meet the performance criteria.

If a controller is not properly tuned, the process variable will eventually reach the setpoint, but the transient response will be different. The transient response is sometimes so aggressive that the loop becomes unstable. So, to verify if a loop is properly tuned, it is not enough to observe the loop at steady state; we must observe the transient response after a change.

The control objective must be specified before tuning a loop. Also, we must decide if the control objective is defined for a load change or a setpoint change. Since a setpoint change is directly applied on the controller and a load change must go through the process and pieces of equipment, a setpoint change is the worst case (more aggressive).

Figure 2 illustrates the difference between aggressive and moderate tuning on setpoint or load change (the scales are identical and the process is a flow loop). If a loop is tuned to respond slowly to a setpoint change, the response will be sluggish for a load change. Different criteria can be used to specify the control objective:

Fast response and minimizing errors: Examples are the Ziegler and Nichols formulas; the quarter amplitude decay corresponds roughly to this definition.
Minimizing the area of the error after a setpoint change or a load change: This can be applied to minimize the integral of absolute error, minimize the integral of the error squared, etc.
Applying a limit to the overshoot after a load change or a setpoint change.
Reaching the setpoint at the maximum speed without overshoot (critical damping).

The differences between aggressive (top) and moderate (bottom) tuning on a setpoint change (left) or load change (right) for a typical flow loop.

These criteria correspond to a specific control objective, giving the desired performance. For each criterion, formulas exist to tune the loop, or software is used to obtain the tuning parameters.

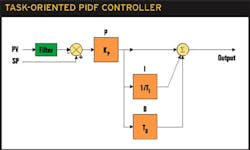
When analyzing the formulas, we observe that the integral time and the derivative time depend mainly on the dead time. The time constant has little or no impact on the controller tuning parameters. This can be explained by the fact that the transient response depends on the dead time.PID ReviewThe proportional-integral-derivative (PID) controller is a well-known algorithm. A PIDF controller includes proportional, integral, derivative, and filter functions:The Proportional (P) part of the PIDF controller is the main part of the algorithm. The output of this part is proportional to the amplitude of the input, usually the error.The Integral (I), also named reset, is used to ensure the process variable will reach the setpoint. The output for this part moves at a speed proportional to the input. The integral time T_Icorresponds to the time needed by the output to move by the same amount as the input.

An ideal proportional-integral-derivative-filter (PIDF) controller may vary in structure but includes a function block for each task.The Derivative (D), also called rate, anticipates the near-future based on the actual slope as its input. The output is proportional to the input speed. The derivative time T_D is the time when the derivative output is before the derivative input (which is a ramp).A Filter (F) component reduces the high-frequency noise often present in the process variable. The filter must be small to ensure it will not increase dead time. The filter time constant (τ_PV) is selected to reduce the process variable noise corresponding to fast disturbances. These fast disturbances cannot be removed by the controller, which is too slow.The figure illustrates a typical controller where each function block is present. The controller structure can be different, but each block has to perform the described task. In this discussion, for the purpose of establishing relationships between the process and the closed loop, we consider an ideal controller such as the one depicted or a series algorithm. The parallel controller is not considered--when using a parallel controller, it is not possible to obtain direct relationship between the process parameters and the integral and derivative time.When to Be SluggishSluggish tuning is sometimes used in processes where all cycling must be eliminated. Tuning loops according to this criterion is rarely recommended. People tuning loops this way are more concerned about setpoint response than about performance to remove a disturbance. They will often choose a closed-loop time constant longer than the process time constant. That way, the process will move slower in automatic mode than in manual mode. Doing so, a disturbance will be removed very slowly and the error will have a large amplitude.Sluggish tuning is useful to synchronize loops, to obtain a nice setpoint response or to obtain sluggish response. This is called the pole-placement method or Lambda tuning. The criterion is defined as moving the process at a speed such that the process will respond as a first-order system,the same behavior as a self-regulating process. For Lambda tuning, the closed-loop time constant recommended is three times the process time constant; this corresponds to a closed loop three times slower than in manual mode.When analyzing the formulas, we observe that the integral time (sluggish tuning will rarely use derivative) depends mainly on the time constant. This is because when we tune a loop that way, we look for the end of the transient response when the process stabilizes, hence the time constant.Tuning a control loop aggressively or moderately implies that the controller parameters will depend mainly on the dead time. The controller and the control loop speed will also depend mainly on the dead time.The Time ScaleWith most processes, the formulas and the methods will generate an integral time that is two to four times the dead time. The integral time will rarely fall outside those limits. Also, the derivative time will be smaller than the dead time and most of the time it will be around half the dead time.The filter time constant (τ_PV) must be smaller than the dead time and smaller than the derivative time. Finally, the sampling time must be a lot smaller than the dead time and preferably smaller than the filter time constant (sample interval < filter < derivative time < dead time < integral time):

t_s< τ_PVT_DT_dT_I

It is also possible to establish a relationship between the dead time and the closed-loop response. The natural period t₀ is the period for unstable conditions: on/off controller, a proportional-only controller with a high gain. This natural period is the maximum speed at which the loop can move. Using less-aggressive tuning to let the process stabilize and reach the setpoint will produce a damped period longer than the natural period; if the tunings are reduced sufficiently, the damped period will disappear. For all processes, the natural period is always between two and four times the dead time:

2t_d < T_O < 4t_d

t_O < t_osc

t_osc ?? 6t_d

t_osc ?? 2T_I

After a setpoint change, a process variable will reach the setpoint after fewer than two or three damped periods. If the cycling is absent, the process variable will reach the setpoint after 10 to 15 times the dead time:

t_set ?? 12t_d

t_set ?? 6T_I

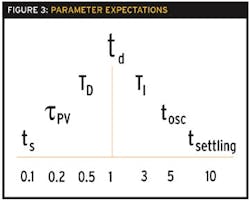
When troubleshooting a control loop, if we know the above relationships, it will be easy to detect abnormalities such as too much integral. Also, just looking at the trends, we can determine if the values make sense. The expected relationships, as shown in Figure 3, are:

t_s< τ_PV< T_D< t_d< T_I < t_osc < t_set

For properly tuned loops, sampling interval t_s, filter time constant τ_PV, derivative time T_D, integral time T_I, damped period t_OSC, and settling time t_set can be expected to lie within well-defined ranges with respect to deadtime t_d.For example, from Figure 2 we have a dead time [t_d] of 5 sec. For aggressive tuning, the settling time on setpoint change is 50 sec. (10 x t_d), the settling time on load change is 60 sec. (12 x t_d), and the damped period t_OSC is 30 sec. (6 x t_d). For moderate tuning the settling time on setpoint change is 45 sec. (9 x t_d), and on load change it's 50 sec. (10 x t_d). In this case, t_OSC does not apply.In ShortWhen observing or a tuning loop, there are several approximations to keep in mind that will quickly tell you whether you are within an order of magnitude. The speed of response in a closed loop is mainly determined by the dead time if the loop is tuned to quickly remove a disturbance. The settling time is roughly 10 times the dead time, and the damped period is about half of the settling time.Controller tuning parameters will mainly be determined by the dead time. The integral time will be roughly two to four times the dead time. The derivative time is half the dead time, and the filter time constant should be selected to be less than 1/5 of the dead time. Finally, the sampling time should be also a fraction of the dead time.If the tuning is too aggressive, divide the proportional gain by two. This will remove the cycling. Dividing it by two again will remove any overshoot that might be present. Most of the time, the integral time and the derivative time will not have to be readjusted unless you are looking for fine tuning.In a control loop, reducing the dead time by half will double performance: Performance is inversely proportional to dead time.Michel Ruel, president of consulting and training firm Top Control, is a university lecturer and author of many publications and books on instrumentation and control. He has 25 years of process plant experience. He may be reached [email protected].